Để giải được bài thi trắc nghiệm Toán trong kỳ thi THPT quốc gia sắp tới, ngoài yếu tố quan trọng là kiến thức và các kĩ năng một yếu tố khác đó là đánh giá nhanh chóng và loại bỏ được các đáp án nhiễu.
- Bày “tuyệt chiêu” ôn thi Địa lý THPT quốc gia có cô Thảo làm giám thị
- Vì sao đề thi trắc nghiệm THPT quốc gia lại có 4 đáp án
- Kinh nghiệm làm bài văn Nghị luận xã hội trong 30 phút.

Điều đó sẽ cho bạn những đáp án chính xác và nhanh chóng hoàn thành để đến với câu hỏi tiếp theo, cuối cùng là hoàn thành bài thi một cách xuất sắc. Dưới đây là một số kinh nghiệm được các thầy giáo đang dạy chuyên toán trường THPT Amsterdam Hà Nội trích ra trong quá trình giảng dạy chương trình ứng dụng đạo hàm. Những kinh nghiệm này sẽ giúp học sinh có thể trả lời nhanh một số câu hỏi liên quan đến hàm số. Đó là cần chú ý đến các dấu hiệu đặc biệt, đặc trưng của từng nội dung trong chương trình.
Trên cơ sở các lý thuyết được đúc rút từ nhiều năm giảng dạy Thầy Đặng Hùng Thanh sẽ giúp các bạn nhận biết được điều đó. Các đấu hiệu được thấy Thanh đề cập ở các hình thức như: Chỉ ra dấu hiệu đặc trưng ở dạng đại số (biểu thức điều kiện), dấu hiệu trực quan (đồ thị, bảng biến thiên và bảng xét dấu)
Dưới đây xin mời các mem 99 tham khảo và luyện tập cho kỳ thi THPT quốc gia môn Toán năm 2017 về nhóm vấn đề này.
Một số hàm thường gặp trong thi trắc nghiệm Toán khách quan:
Hàm số bậc ba


Các dấu hiệu và các trường hợp đặc biệt các bạn cần ghi nhớ:

Ví dụ minh họa:





Hàm số trùng phương


Các dấu hiệu và các trường hợp đặc biệt cần ghi nhớ: Hàm số trùng phương có 1 cực trị hoặc 3 cực trị. Nếu a và b trái dấu có 3 cực trị: một tại x = 0 và tại hai điểm đối nhau. Nếu a và b cùng dấu dấu có 1 cực trị tại x = 0. Luôn có cực trị tại x = 0. Đồ thị nhận trục tung làm trục đối xứng.
Các ví dụ minh họa:



Hàm bất biến


Dấu hiệu và tính chất đặc trưng cần ghi nhớ


Bài tập áp dụng:



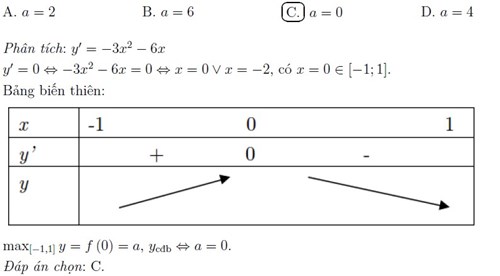
Giá trị lớn nhất và nhỏ nhất của hàm số trong đề thi trắc nghiệm Toán THPT quốc gia
Cho hàm số y = f(x), có tập xác định D. Phương pháp chung để tìm giá trị lớn nhất, giá trị nhỏ nhất bằng cách sử dụng đạo hàm:
Lập bảng biến thiên của hàm số trên D. Dựa vào bảng biến thiên: kết luận giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Các dấu hiệu và các trường hợp đặc biệt cần ghi nhớ:


Ví dụ minh họa:



Nhớ theo dõi thông tin tuyển sinh trên THPT quốc gia để cập nhật những kiến thức mới nhất về kì thi sắp tới.
Lam hạ (theo thptquocgia.org)
